Non-well-founded set theory
Non-well-founded set theories are variants of axiomatic set theory which allow sets to contain themselves and otherwise violate the rule of well-foundedness. In non-well-founded set theories, the foundation axiom of ZFC is replaced by axioms implying its negation.
The theory of non-well-founded sets has been applied in the logical modelling of non-terminating computational processes in computer science (process algebra and final semantics), linguistics and natural language semantics (situation theory), philosophy (work on the Liar Paradox), and in a different setting, non-standard analysis.[1]
Contents |
Details
- A set, x0, is well-founded iff it has no infinite descending membership sequence:
- · · ·
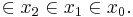
- · · ·
In ZFC, there is no infinite descending ∈-sequence by the axiom of regularity. In fact, the axiom of regularity is often called the foundation axiom since it can be proved within ZFC− (that is, ZFC without the axiom of regularity) that well-foundedness implies regularity. In variants of ZFC without the axiom of regularity, the possibility of non-well-founded sets with set-like ∈-chains arises. For example, a set A such that A ∈ A is non-well-founded.
One early non-well-founded set theory was Willard Van Orman Quine’s New Foundations. Another was introduced by Maurice Boffa, with the idea of making foundation fail as badly as it can (or rather, as extensionality permits): Boffa's axiom implies that every extensional set-like relation is isomorphic to the elementhood predicate on a transitive class.
Another, more recent, approach to non-well-founded set theory, pioneered by M. Forti and F. Honsell, borrows from computer science the concept of a bisimulation. Bisimilar sets are considered indistinguishable and thus equal, which leads to a strengthening of the axiom of extensionality. In this context, axioms contradicting the axiom of regularity are known as anti-foundation axioms, and a set that is not necessarily well-founded is called a hyperset.
Four non-equivalent anti-foundation axioms are well-known:
- AFA (‘Anti-Foundation Axiom’) — due to M. Forti and F. Honsell (this is also known as Aczel's anti-foundation axiom);
- SAFA (‘Scott’s AFA’) — due to Dana Scott,
- FAFA (‘Finsler’s AFA’) — due to Paul Finsler,
- BAFA ('Boffa's AFA') — due to Maurice Boffa.
The first of these, AFA, is based on accessible pointed graphs (apg) and states that two hypersets are equal if and only if they can be pictured by the same apg. Within this framework, it can be shown that the so-called Quine atom, formally defined by Q={Q}, exists and is unique.
Each following axiom extends the universe of the previous, so that: V ⊆ A ⊆ S ⊆ F ⊆ B. In the Boffa universe, the distinct Quine atoms form a proper class. [2]
It is worth emphasizing that hyperset theory is an extension of classical set theory rather than a replacement: the well-founded sets within a hyperset domain conform to classical set theory.
Notes
References
- Aczel, Peter (1988), Non-well-founded sets, CSLI Lecture Notes, 14, Stanford, CA: Stanford University, Center for the Study of Language and Information, pp. xx+137, ISBN 0-937073-22-9, MR0940014, http://standish.stanford.edu/pdf/00000056.pdf.
- Ballard, David; Hrbáček, Karel (1992), "Standard foundations for nonstandard analysis", Journal of Symbolic Logic 57 (2): 741–748, doi:10.2307/2275304, JSTOR 2275304.
- Hallett, Michael (1986), Cantorian set theory and limitation of size, Oxford University Press.
- Levy, Azriel (2002), Basic set theory, Dover Publications.
- Mirimanoff, D. (1917), "Les antinomies de Russell et de Burali-Forti et le probleme fondamental de la theorie des ensembles", L'Enseignement Mathématique 19: 37–52, http://retro.seals.ch/digbib/view?rid=ensmat-001:1917:19::9&id=hitlist.
- Nitta; Okada; Tzouvaras (2003), Classification of non-well-founded sets and an application, http://users.auth.gr/~tzouvara/Texfiles.htm/non-well.pdf
See also
External links
- Lawrence S. Moss (2008-04-16), "Non-wellfounded Set Theory", Stanford Encyclopedia of Philosophy, http://plato.stanford.edu/entries/nonwellfounded-set-theory/
- Metamath page on the axiom of Regularity. Scroll to the bottom to see how few Metamath theorems invoke this axiom.